网站建设沙漠风口碑营销成功案例

目录
1. 路径交叉 ★★★
2. 缺失的第一个正数 ★★★
3. 寻找两个正序数组的中位数 ★★★
附录
散列表
基本概念
常用方法
1. 路径交叉
给你一个整数数组 distance 。
从 X-Y 平面上的点 (0,0) 开始,先向北移动 distance[0] 米,然后向西移动 distance[1] 米,向南移动 distance[2] 米,向东移动 distance[3] 米,持续移动。也就是说,每次移动后你的方位会发生逆时针变化。
判断你所经过的路径是否相交。如果相交,返回 true ;否则,返回 false 。
示例 1:
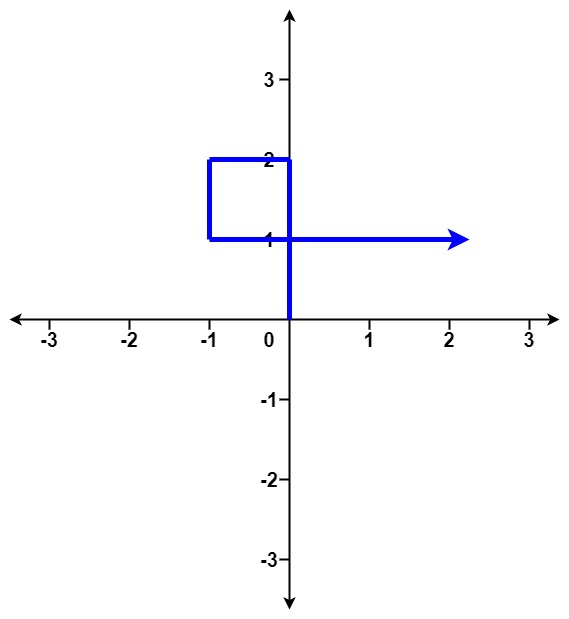
输入:distance = [2,1,1,2] 输出:true
示例 2:
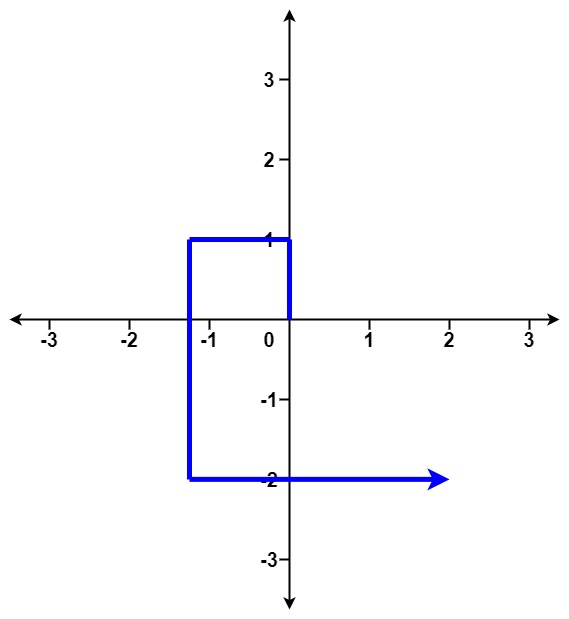
输入:distance = [1,2,3,4] 输出:false
示例 3:
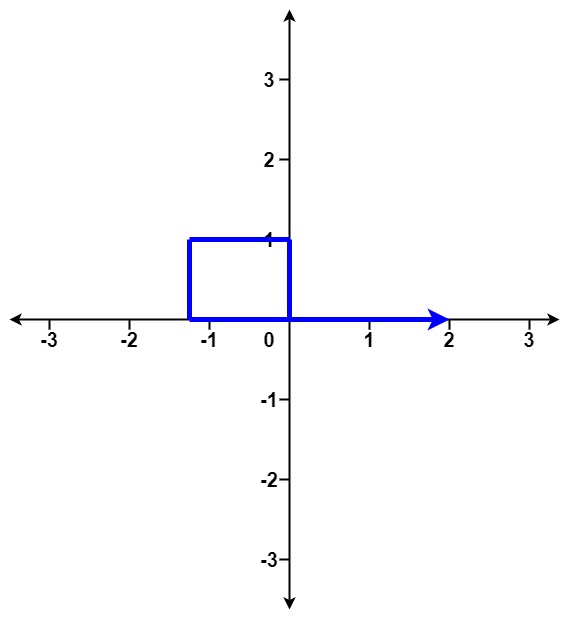
输入:distance = [1,1,1,1] 输出:true
提示:
1 <= distance.length <= 1051 <= distance[i] <= 105
代码:
class Solution:def isSelfCrossing(self, x: list) -> bool:n = len(x)if n < 3: return Falsefor i in range(3, n):if x[i] >= x[i - 2] and x[i - 3] >= x[i - 1]: return Trueif i >= 4 and x[i - 3] == x[i - 1] and x[i] / x[i - 4] >= x[i - 2]: return Trueif i >= 5 and x[i - 3] >= x[i - 1] and x[i - 2] >= x[i - 4] and x[i - 1] + x[i - 5] >= x[i - 3] and x[i] + x[i - 4] >= x[i - 2]: return Truereturn Falses = Solution()
distance = [2,1,1,2]
print(s.isSelfCrossing(distance))distance = [1,2,3,4]
print(s.isSelfCrossing(distance))distance = [1,1,1,1]
print(s.isSelfCrossing(distance))输出:
True
False
True
2. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
进阶:你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗?
示例 1:
输入:nums = [1,2,0] 输出:3
示例 2:
输入:nums = [3,4,-1,1] 输出:2
示例 3:
输入:nums = [7,8,9,11,12] 输出:1
提示:
0 <= nums.length <= 300-2^31 <= nums[i] <= 2^31 - 1
代码:
class Solution(object):def firstMissingPositive(self, nums):ls = len(nums)index = 0while index < ls:if nums[index] <= 0 or nums[index] > ls or nums[nums[index] - 1] == nums[index]:index += 1else:pos = nums[index] - 1nums[index], nums[pos] = nums[pos], nums[index]res = 0while res < ls and nums[res] == res + 1:res += 1return res + 1# %%
s = Solution()
print(s.firstMissingPositive(nums = [1,2,0]))
print(s.firstMissingPositive(nums = [3,4,-1,1]))
print(s.firstMissingPositive(nums = [7,8,9,11,12]))输出:
3
2
1
3. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
示例 3:
输入:nums1 = [0,0], nums2 = [0,0] 输出:0.00000
示例 4:
输入:nums1 = [], nums2 = [1] 输出:1.00000
示例 5:
输入:nums1 = [2], nums2 = [] 输出:2.00000
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-10^6 <= nums1[i], nums2[i] <= 10^6
代码:
import math
from typing import Listclass Solution:def findMedianSortedArrays(self, nums1: List[int],nums2: List[int]) -> float:nums1Size = len(nums1)nums2Size = len(nums2)na = nums1Size + nums2Sizens = []i = 0j = 0m = int(math.floor(na / 2 + 1))while len(ns) < m:n = Noneif i < nums1Size and j < nums2Size:if nums1[i] < nums2[j]:n = nums1[i]i += 1else:n = nums2[j]j += 1elif i < nums1Size:n = nums1[i]i += 1elif j < nums2Size:n = nums2[j]j += 1ns.append(n)d = len(ns)if na % 2 == 1:return ns[d - 1]else:return (ns[d -1] + ns[d - 2]) / 2.0# %%
s = Solution()
print(s.findMedianSortedArrays([1,3], [2]))
print(s.findMedianSortedArrays([1,2], [3,4]))
print(s.findMedianSortedArrays([0,0], [0,0]))
print(s.findMedianSortedArrays([], [1]))
print(s.findMedianSortedArrays([2], []))输出:
2
2.5
0.0
1
2
附录
散列表
Hash table,也叫哈希表,是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
基本概念
若关键字为k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系f为散列函数,按这个思想建立的表为散列表。
对不同的关键字可能得到同一散列地址,即k1≠k2,而f(k1)==f(k2),这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就是使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
常用方法
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。实际工作中需视不同的情况采用不同的哈希函数,通常考虑的因素有:
· 计算哈希函数所需时间
· 关键字的长度
· 哈希表的大小
· 关键字的分布情况
· 记录的查找频率
1.直接寻址法:
取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。
2. 数字分析法:
分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3. 平方取中法:
当无法确定关键字中哪几位分布较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以较高的概率产生不同的哈希地址。
4. 折叠法:
将关键字分割成位数相同的几部分,最后一部分位数可以不同,然后取这几部分的叠加和(去除进位)作为散列地址。数位叠加可以有移位叠加和间界叠加两种方法。移位叠加是将分割后的每一部分的最低位对齐,然后相加;间界叠加是从一端向另一端沿分割界来回折叠,然后对齐相加。
5. 随机数法:
选择一随机函数,取关键字的随机值作为散列地址,即H(key)=random(key)其中random为随机函数,通常用于关键字长度不等的场合。
6. 除留余数法:
取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p≤m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
